Erdbebenstärke – Magnitude – Richterskala

lokale Magnitude – Richterskala

Die Stärke eines Erdbebens  ist abhängig von der Menge der freigesetzten seismischen Energie (E_s). Um die Stärke eines Bebens anzugeben wurde von Richter (1935) die logarithmische Magnitudenskala entwickelt. Die lokale Magnitude (M_l; Magnitude auf der Richterskala) kann mittels der maximalen Amplitude (A_max) der horizontalen Komponente, die von einem Wood-Anderson-Torsionsseismometer aufgezeichnet wurde, errechnet werden [Richter 1935]:

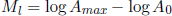
log A₀ ist ein Kalibrierwert, der vom Epizentralabstand  abhängig ist. Zudem gelten für unterschiedliche Regionen der Erde unterschiedliche Kalibrierwerte. Der Epizentralabstand darf für die Berechnung der lokalen Magnitude nicht größer als 600 km sein.

Oberflächenwellen-Magnitude

Die Oberflächenwellen-Magnitude (M_s) kann mittels teleseismischer Oberflächenwellen bestimmt werden, wenn der Epizentralabstand (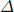) zwischen 2° und 160° liegt. Zudem darf der Erdbebenherd  in maximal 50 km Tiefe liegen. Mittels der maximalen Bodenpartikelgeschwindigkeit ((A/T)_max, max.(Amplitude / Periode)) lässt sich die Oberflächenwellen-Magnitude berechnen [Karnik et al. 1962]:

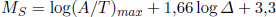
Moment-Magnitude

Bei starken Beben kann es zu einer Sättigung der Amplitude kommen, dadurch ist die Proportionalität z.B. der Oberflächenwellen-Magnitude zur Stärke des Bebens bei starken Erdbeben nicht mehr gegeben. Bei Beben, bei denen die Sättigung nicht erreicht ist, ist die Moment-Magnitude (M_w) etwa gleich der Oberflächenwellen-Magnitude (M_s). Im Unterschied zu dieser erreicht die Moment-Magnitude aber keine Sättigung, da sie sich aus der horizontalen Ausdehnung der Herdfläche oder der Länge der Erdbebenherdfläche entlang des Einfallens errechnen lässt.

weitere Magnituden

Daneben gibt es noch weitere Möglichkeiten die Magnitude zu ermitteln, z.B. aus teleseismischen Raumwellen (m_B).

Beziehung zwischen den Magnituden und der Energie

Die Beziehung zwischen der lokalen Magnitude und der Oberflächenwellen-Magnitude ist nach Gutenberg und Richter wie folgt [Gutenberg und Richter 1956a]:

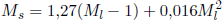
Aus der Magnitude kann die freigesetzte seismische Energie (E_s in Joule) errechnet werden [Gutenberg und Richter 1956b]:

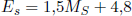
Seismische Moment

Ein weiteres Maß für die Stärke eines Bebens ist das seismische Moment (M₀), da es die irriversible Deformation des Bruchs angibt [Aki und Richards 1980]:

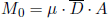
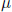ist das Schermodul des Mediums, 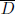die durchschnittliche Verschiebung nach dem Bruch und A ist die Bruchfläche.

Der Vorteil des seismischen Moments ist, dass es von den Herdparametern abhängt und nicht aus der gemessenen Seismogrammamplitude  ermittelt wird. Bei dem seismischen Moment tritt eine Sättigung hingegen nicht auf, da keine Seismogrammamplitude zur Ermittlung des Wertes herangezogen wird.

Die Beziehung zwischen der freigesetzten seismischen Energie und dem seismischen Moment ist nach Kanamori [Kanamori 1977]:

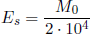
Aus dem seismischen Moment lässt sich die Oberflächenwellen-Magnitude errechnen ([Ekström und Dziewonski 1988], [Chen und Chen 1989]).